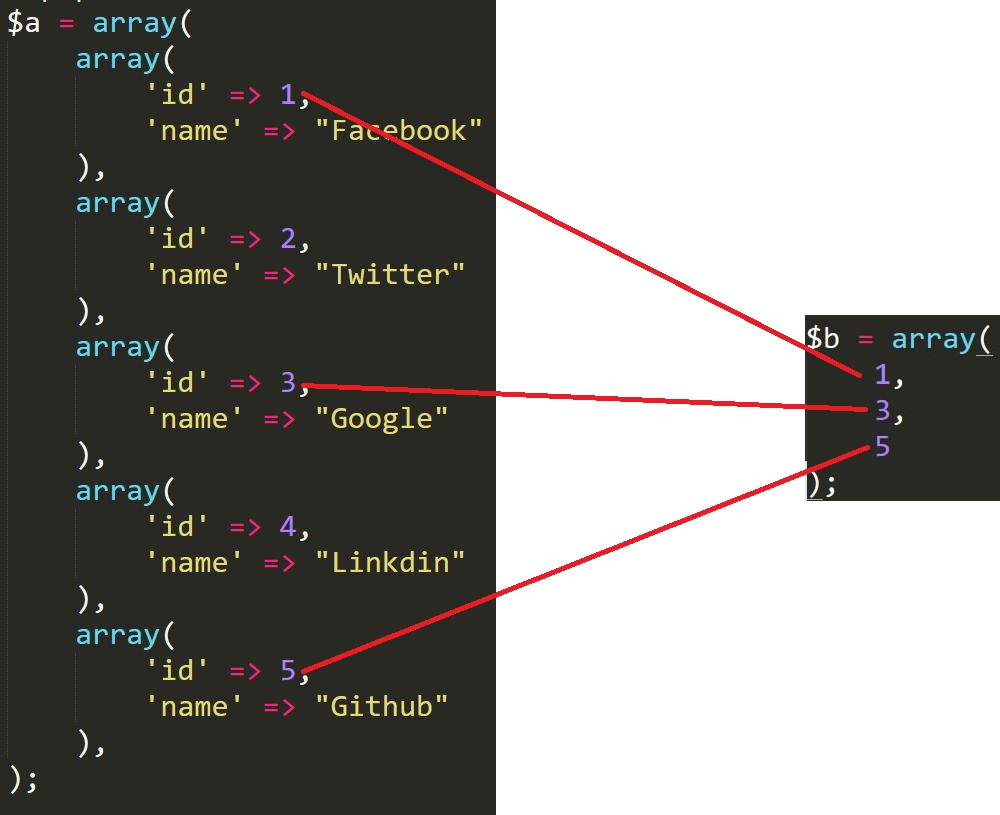
A group of related data pieces stored in contiguous memory locations is an array. It is the most basic data structure in which each data element is accessible simply by its index number alone.
For example, if we want to keep a student’s grades in five subjects, we don’t need to establish distinct variables for each topic.
We can instead build an array that stores the data items in contiguous memory locations.
Marks[0] denotes the marks scored in the first subject, marks[1] denotes the marks scored in the second subject, and so on. Array marks[5] denotes the marks scored by a student in 5 different subjects, where each subject marks are located at a specific location in the array, i.e. marks[0] denotes the marks scored in the first subject, marks[1] denotes the marks scored in the second subject, and so on.
Need of using it
In most circumstances, programming requires the storage of a huge amount of data of a comparable type.
We need to define a lot of variables to store such a large amount of data. While writing the scripts, it would be quite difficult to remember all of the variable names. It is preferable to create an array and store all of the elements in it.
The following example demonstrates how they can be utilized in code-writing:
We’ve given a student’s grades in five distinct subjects in the example below. The goal is to find the average of a student’s grades.
Without using it
|
2
3
4
5
6
7
|
#include<stdio.h>void main(){ int subject1 = 40, subject2 = 52, subject3 = 47, subject4 = 70, subject5= 67; float avg = (subject1 + subject2 + subject3 + subject4 + subject5)/5; printf(avg);} |
Using array
|
2
3
4
5
6
7
|
#include<stdio.h>void main(){ int subject1 = 40, subject2 = 52, subject3 = 47, subject4 = 70, subject5= 67; float avg = (subject1 + subject2 + subject3 + subject4 + subject5)/5; printf(avg);} |
Complexity of Array Operations
Time Complexity
| Algorithm | Average case | Worst case |
| Access | O(1) | O(1) |
| Search | O(n) | O(n) |
| Insertion | O(n) | O(n) |
| Deletion | O(n) | O(n) |
Space complexity of an array for the worst case is O(n).
Advantages of arrays
- They use a single identifier to represent numerous data elements of the same type.
- Using the index number to retrieve or find an element in an array is simple.
- The index of an array can be easily incremented by one to traverse it.
- For all of its data elements, arrays allocate memory in contiguous memory regions.
Types of indexing in arrays
- 0 (Zero Based Indexing) – The first element of it refers to index 0.
- 1 (One Based Indexing) – The first element of it refers to index 1.
- n (n Based Indexing) – The base index of it can be chosen as per requirement.

Accessing Elements in it
To access any element of an array we need the following details:
- Base Address.
- Size of an element in bytes.
- Which type of indexing it follows.
The following formula can be used to calculate the address of any element in a 1D array:
Byte address of an element A[i] = base address + size * (i – first index)
Passing Array to a Function
As previously stated, the address of the its first element is represented by the array’s name. The base address can be used to traverse the items of an array.
The following example shows how to provide an array to a function.
The program below defines the total function, which takes it as an input.
This function computes the sum of all the array’s items.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include<stdio.h>int total(int[]);void main(){ int arr[5] = {0,1,2,3,4}; int sum = total(arr); printf(“%d”,sum);}int total(int arr[]){ int sum=0; int i; for(i=0; i<5; i++) { sum = sum + arr[i]; } return sum;} |
2D Array– Defined
An array of arrays is a common definition for a T2-dimensional array. A matrix is another name for a two-dimensional array. A matrix looks like a table with rows and columns.
How to declare 2D Array?
Declaring a 2D follows the same syntax as declaring a 1D array.
Syntax –
int arr[max_rows][max_columns];
It produces data structure as shown below:

How to access data in a 2D ?
In the same way that data may be accessed using simply an index in a one-dimensional array, the indices of the cells can be used to access the cells individually in a two-dimensional array. A single cell has two indices: one is its row number, and the other is its column number.
Syntax to store the value stored in any particular cell of it–
int x = a[i][j];
Here i and j are the row and column indices respectively
Initializing 2D array
When declaring a one-dimensional, we don’t need to mention its size, but this isn’t the case with a two-dimensional. We must define at least the row size, or the second dimension, for a 2D.
Syntax to declare 2D –
int arr[2][2] = {1,2,3,4}
The number of elements present in a 2D will always be equal to (number of rows * number of columns).
Mapping 2D to 1D array
2D arrays are mostly used to construct a data structure that resembles a database table. The storing strategy for 2D in computer memory is identical to that of a one-dimensional.
The product of the number of rows and the number of columns in a 2D is always equal to its size.
As a result, in order to store two-dimensional in memory, we must map them to one-dimensional arrays.
A 3 X 3 2D are shown in the image below.

There are 2 main techniques to map a two dimensional array to one dimensional array
- Row Major Ordering
All the rows of the two dimensionals are stored in a continuous way in memory when row major ordering is used. The memory allocation for it is displayed in the preceding image using the row major order technique is illustrated below.

The first row of the 2D is inserted into memory first, followed by the items of the second row, and so on.
2. Column Major Ordering
All of the columns of the two-dimensional array are stored in the memory in a continuous manner in column major ordering. The memory allocation for the array displayed in the preceding image using the column major order technique is illustrated below.

The elements of the first column of the 2D array are first inserted into memory, followed by the elements of the second column, and so on.
Don’t miss our interesting and useful topics. Just click here and find out more.
Also watch this YouTube video related to Arrays.